Dogs, pointing and causal inference

What's so special about the cognitive abilities of domestic dogs? This has been a long-standing question, perhaps the question, since the boom of dog behaviour and cognition research 25 to 30 years ago. The obvious answer is that dogs are highly attuned to read and respond to human behaviour on account of convergent evolution with humans over some 15,000-plus years. Surely, the first animal to be domesticated has something to show for their tolerance of human company all those years? This has come to be known as the 'domestication hypothesis'.

A common experimental paradigm to test whether domestic dogs have evolved abilities to read human behaviour is the human pointing study (for instance, see Miklósi & Soproni, 2005 or Dorey et al. 2009 or Udell, 2010 or Wynne, 2016). Dogs are placed in front of a human who has containers of food to their left and right. Over a number of trials, humans point to different containers, in a variety of ways, and researchers test the hypothesis that dogs follow the human point more often than chance to the pointed-to container.

Where this gets interesting is in studies that compare dogs and wolves. Wolves have generally performed worse than dogs in human pointing studies (see, for example, Virányi et al. 2008) and researchers have used these results to support the hypothesis that dogs have evolved specifically to live with humans and follow their communicative signals. But over the last 10 years, this has been subject to a classic nature or nurture debate, a question of, technically, phylogeny or ontogeny. Are dogs genetically-predisposed to perform better at this task than wolves, or can their superior performance be explained by lifestyle factors that mean dogs have more exposure to humans than their wolf counterparts?

Obviously, one would need to put dogs and wolves on equal environmental footing to test this hypothesis properly. But, that's not always so easy to do, since facilities where wolves and dogs have the exact same upbringing are not plentiful, and dogs will at some stage be placed in human homes where wolves will not. These constraints on executing randomised controlled trials, or not, is where good statistical decisions are important.

In 2023, Wheat, Bijl & Wynne re-analysed data from Salomons et al. (2021) who reported that hand-raised wolves performed worse than dogs on a few different standardised tests, including a human pointing task. The study also posited that while the number of times subjects approached familiar and unfamiliar people and objects — referred to as temperament during the study — was positively associated with point-following performance, the relationship vanished when species was included into the regression model. The species effect was also no longer significant when including both temperament and species in the same model. Wheat, Bijl & Wynne's re-analysis indicated that the differences between wolves and dogs in human point-following only emerged in dogs after being homed with human families at 8 weeks of age. Wheat, Bilj & Wynne also re-fit a model explaining point-following performance with species and temperament as predictor variables. They found no appreciable differences in out-of-sample predictive accuracy using Akaike's Information Criteria (AIC) between models with or without species and/or temperament as covariates.

There's quite a lot to unpack here, statistically, but it's helpful and illuminating to place the results under a causal lens.

The domestication hypothesis says that domestication and, therefore, species — dogs or wolves — has a direct causal effect on point-following performance. According to Salomons et al. (2021), species also influences a willingness to approach unfamiliar humans or objects. On the other hand, in what I will call here the 'developmental' hypothesis, dogs and wolves experience different rearing conditions (i.e. exposure to humans), which influences willingness to engage with humans and, ultimately, point-following performance. Thus, the causal effect of species is mediated by rearing experience and willingness to approach. This is the crux of Wheat, Bilj & Wynne's argument.

We can compare these hypotheses visually using directed acyclic graphs, which could look something like this, where P stands for point-following performance, W represents 'willingness to approach strangers', S is species, and R is the rearing environment.

In the domestication hypothesis, because species is a common cause of both willingness to approach strangers and point-following performance, any effect of willingness to approach strangers should disappear when species is conditioned upon. To demonstrate this, I simulated data according to the following simplified model of the domestication hypothesis.

The index $i=1,...,N$ represents individual dogs, $n$ is the number of trials of the point-following task per dog, and $P$, $W$ and $S$ are as above. I am ignoring control conditions and different types of gestures here, and only imagining that dogs receive $n$ trials of one point-following task on which to gauge their performance. I also assume that $S$ and $W$ are Bernoulli variables, standing for wolves (0) or dogs (1) and no-approach (0) and approach (1), respectively. Here's what this data generating process looks like in Python, choosing some values for the constants.

import numpy as np

SEED = 1234
rng = np.random.default_rng(SEED)

def ilogit(x: np.ndarray) -> np.ndarray:
    return np.array([
        1 / (1 + np.exp(-i))
        for i
        in x
    ])

N = 500
n = 6
b_sw_w = 0
b_sw_d = 3.5
b_sp_w = 0.5
b_sp_d = 1.3

S = rng.binomial(n=1, p=0.5, size=N)
theta = ilogit(b_sw_d * S + b_sw_w * (1 - S))
W = rng.binomial(n=1, p=theta)
pi = ilogit(b_sp_d * S + b_sp_w * (1 - S))
P = rng.binomial(n=n, p=pi)

I am setting N=500 to ensure there is a big enough sample size to estimate the effects of interest, which assumes that on average there will be 250 dogs and 250 wolves. This is considerably larger than Salomons et al.'s sample size. The logit-scale probabilities of dogs and wolves approaching unfamiliar humans, b_sw_d and b_sw_w, are set to match the results of Salomons et al. who reported a 30 fold increase in log odds for dogs approach unfamiliar people compared to wolves. Finally, the logit-scaled probabilities b_sp_d and b_sp_w represent point-following success per species, and are set to approximately 62% for wolves and 78% for dogs, roughly matching the study's results.

I then fit a binomial regression model similar to the paper, with both species and willingness to approach as predictors. One key difference is that the original authors used a Bernoulli regression model with random effects per subject to capture trial-level effects, but we don't need to worry about that because we have no trial-level data. Here's the model mathematically with weakly-informative priors.

$$ \begin{align} P_i &\sim \mathrm{Binomial}(n, \eta_i)\\ \eta_i &= \mathrm{ilogit}^{-1}( \alpha + \beta_S (S_i - 0.5) + \beta_W (W_i - 0.5) )\\ \alpha &\sim \mathrm{Normal}(0, 5)\\ \beta_S &\sim \mathrm{Normal}(0, 1)\\ \beta_W &\sim \mathrm{Normal}(0, 1)\\ \end{align} $$

I have used slightly different notation to avoid conflating the parameters with the true causal model. I have also made the Bernoulli variables $S$ and $W$ take values $(-0.5, 0.5)$ to help the interpretation of $\alpha$ as close to the average logit success. Here's the model written and estimated in PyMC.

import pymc as pm

with pm.Model() as _:
    alpha = pm.Normal("alpha", mu=0, sigma=5)
    beta_S = pm.Normal("beta_S", mu=0, sigma=1)
    beta_W = pm.Normal("beta_W", mu=0, sigma=1)
    eta = pm.math.invlogit(
        alpha + 
        beta_S * (S - 0.5) +
        beta_W * (W - 0.5)
    )
    pm.Binomial("P", n=n, p=eta, observed=P)
    idata = pm.sample(1000, tune=1000, random_seed=rng)

This model returns the following posterior distributions of $\beta_{S}$ and $\beta_{W}$ on point-following performance, along with the true, direct causal effects and the 94% highest density intervals (HDIs).

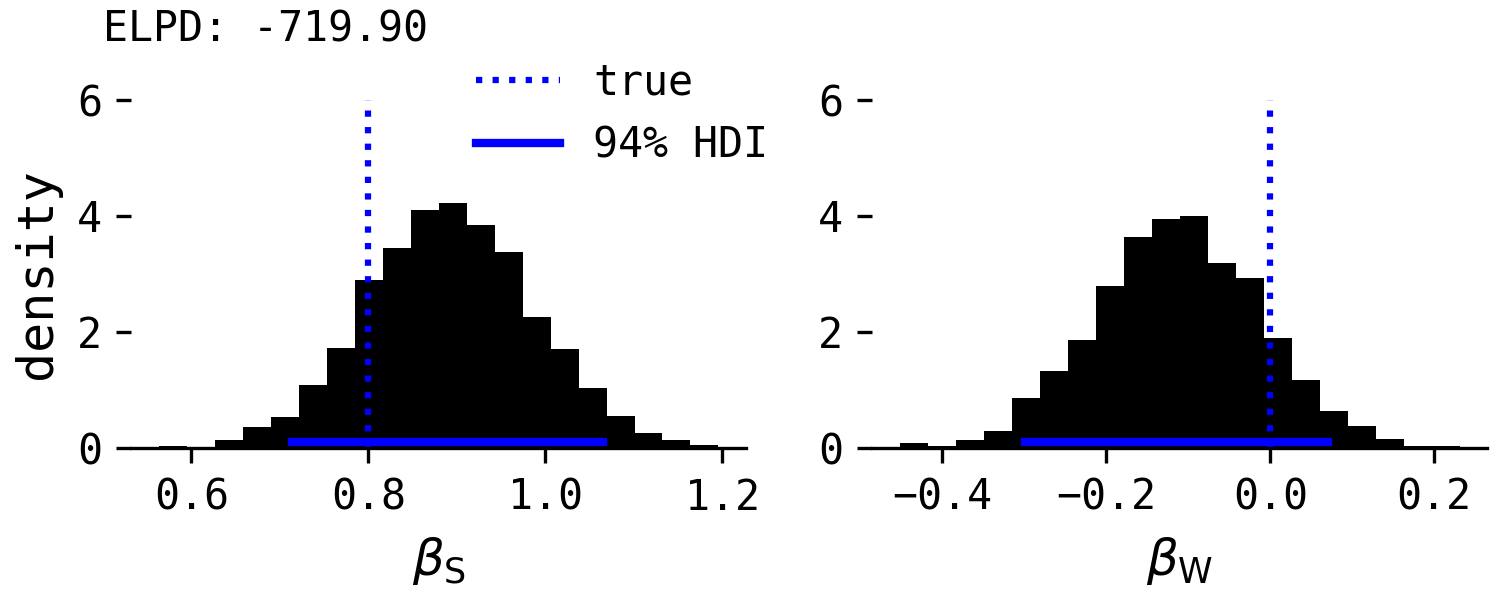
As expected by the causal model, species is 'significant', in that its HDI is clearly positive, and the effect of willingness is close to zero. Note, however, in this particular simulation, the estimation of $\beta_W$ is on average negative, which will be important later. Like Salomons et al. found, the effect of willingness is therefore conditional upon species. However, unlike Salomons et al., species remains an important predictor of point-following, whereas the authors reported that the species effect was curtailed in the combined 'species and willingness' regression model. This is not in support of the domestication hypothesis.

If separate regressions for each predictor were run, the following results would be found.

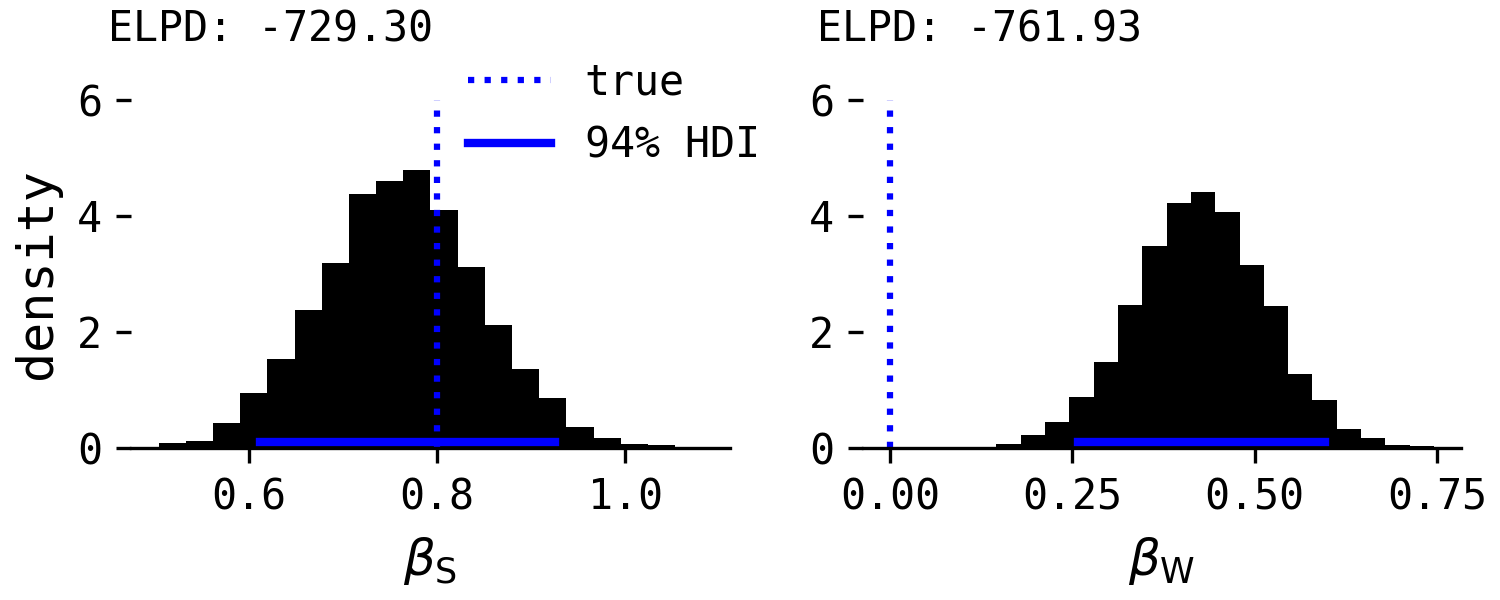
As found in Salomons et al., both predictors are significant when included without the other.

In their re-analysis, Wheat, Bilj & Wynne argued that neither combined nor separate regression models could be decided between because of their equivalent AIC values. In the above models, the expected log predictive density, ELPD, a measure of out-of-sample predictive accuracy and a Bayesian analogue to AIC, favours the first model, despite willingness in reality having no causal effect. Why? Because the estimate of $\beta_W$ in the first model, while not 'significant', seems to have some small average, negative affect on point-following performance, which in this instance is just statistical noise. Optimising for predictive accuracy does not necessarily align with causal accuracy, and this highlights the dangers of Wheat, Bilj & Wynne's focus on AIC values to provide evidence for one or the other hypothesis.

Let's do the same for the developmental hypothesis. If you're interested in the simulation code, you can see it at the Github repository. First, here's the regression including both predictors.

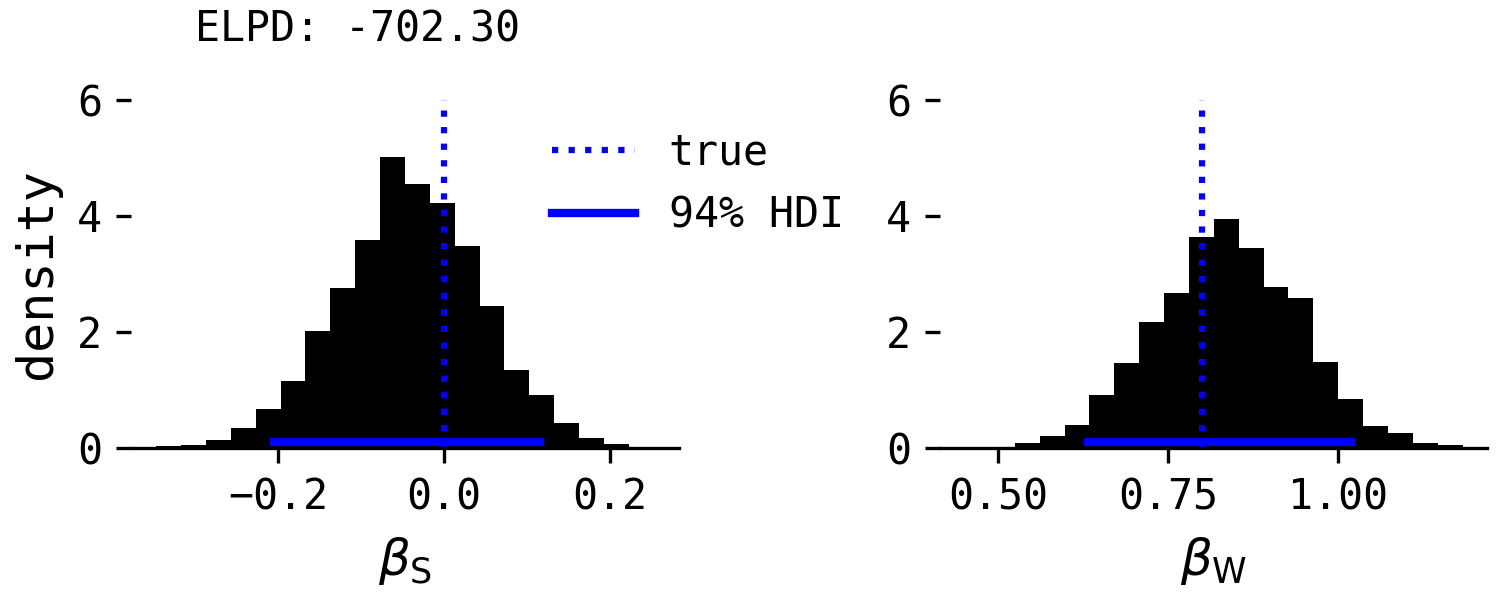
The effect of species is close to zero and the effect of willingness is plausibly above zero, because willingness has a direct causal effect on point-following. Wheat, Bilj & Wynne say little about this in their commentary, but if the developmental hypothesis was correct, we'd expect an effect of willingness to be present when conditioning on species, not disappear as in the domestication hypothesis.

Here are the results for the separate regressions.

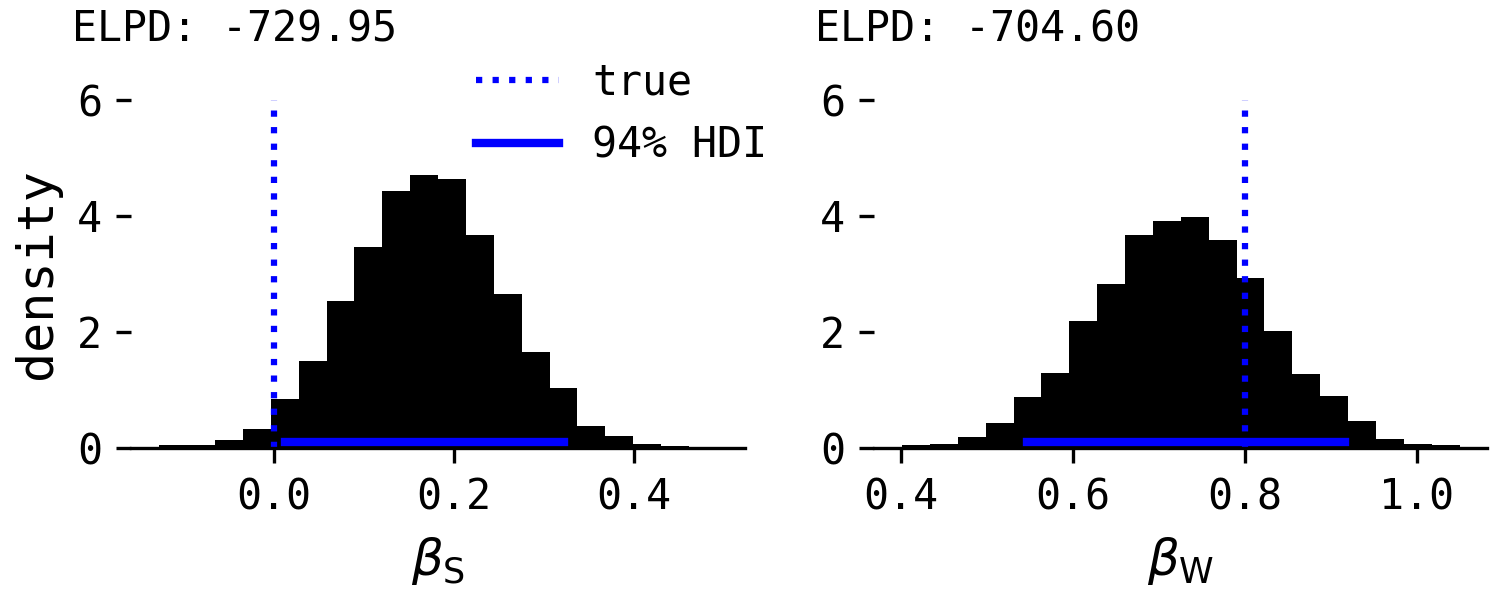
Now $\beta_S$ has a small but positive effect and $\beta_W$ is also accurately estimated. The ELPD values again slightly favour the combined regression because of the small average, non-zero effect of species, despite the real causal effect being zero.

Finally, let's see what happens when we include rearing experience, R, into the regression as well.

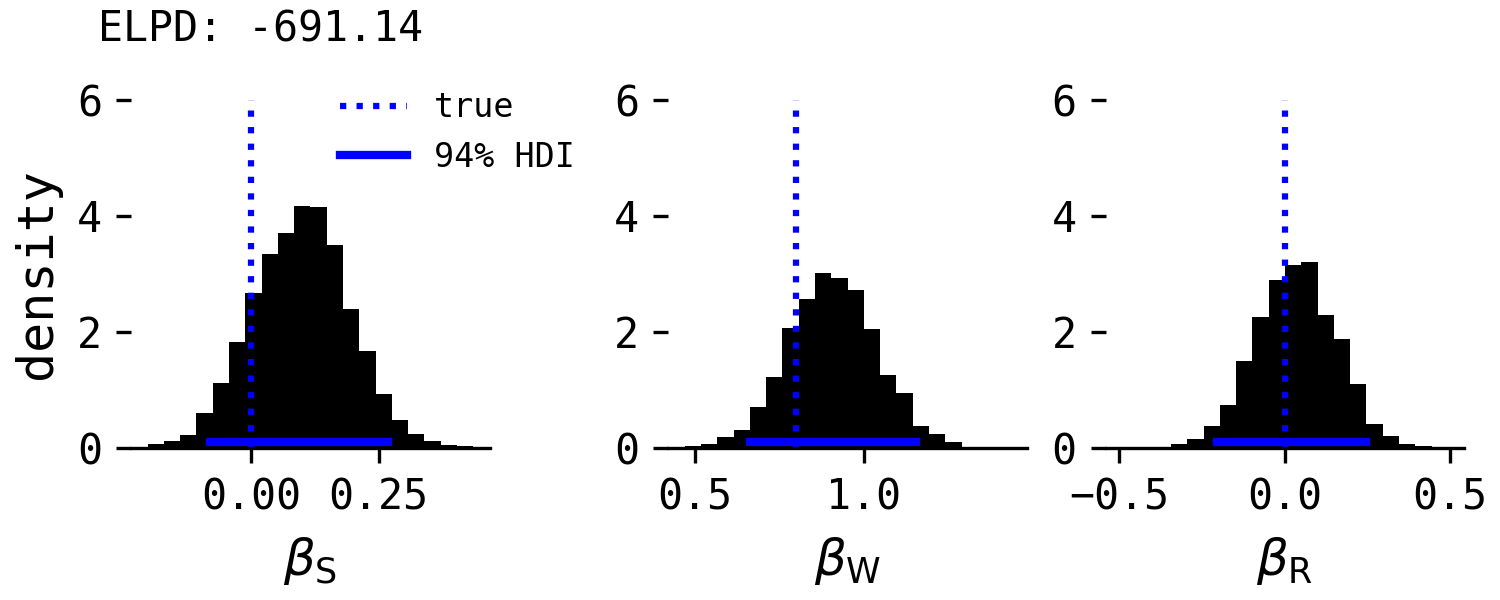
This model correctly indicates that species and rearing experience have no direct causal effect on point-following when conditioning on willingness to approach, and clearly wins on ELPD.

To my knowledge, no-one has fit this model to the original dataset. Wheat, Bilj & Wynne found that rearing influenced point-following in a model conditioning on only species, which is expected by the developmental hypothesis causal model, but the effect should disappear when conditioning on willingness to approach. This would be a simple yet powerful test of their hypothesis. If I have time, I will dig out the original data.

Sample size and power

Most canine cognition studies are underpowered (Ardens et al., 2016) but Salomons et al. boasts one of the largest sample sizes in a study of its kind, with 44 dogs and 37 wolves. Wheat, Bilj & Wynne even praise the large sample size. However, whether a sample size is large enough is dependent on the data-generating assumptions and decision criteria.

I conducted a simple simulation study of the domestication and developmental hypotheses using a variety of sample sizes, simulating 1000 datasets at each sample size. The models were fit using MLE for speed. Here are the results, where the y axis shows the probability of correct inference, whether that's a true positive/direct causal effect or a true negative/no direct effect. The former is traditionally known as 'power', and the latter often gets ignored.

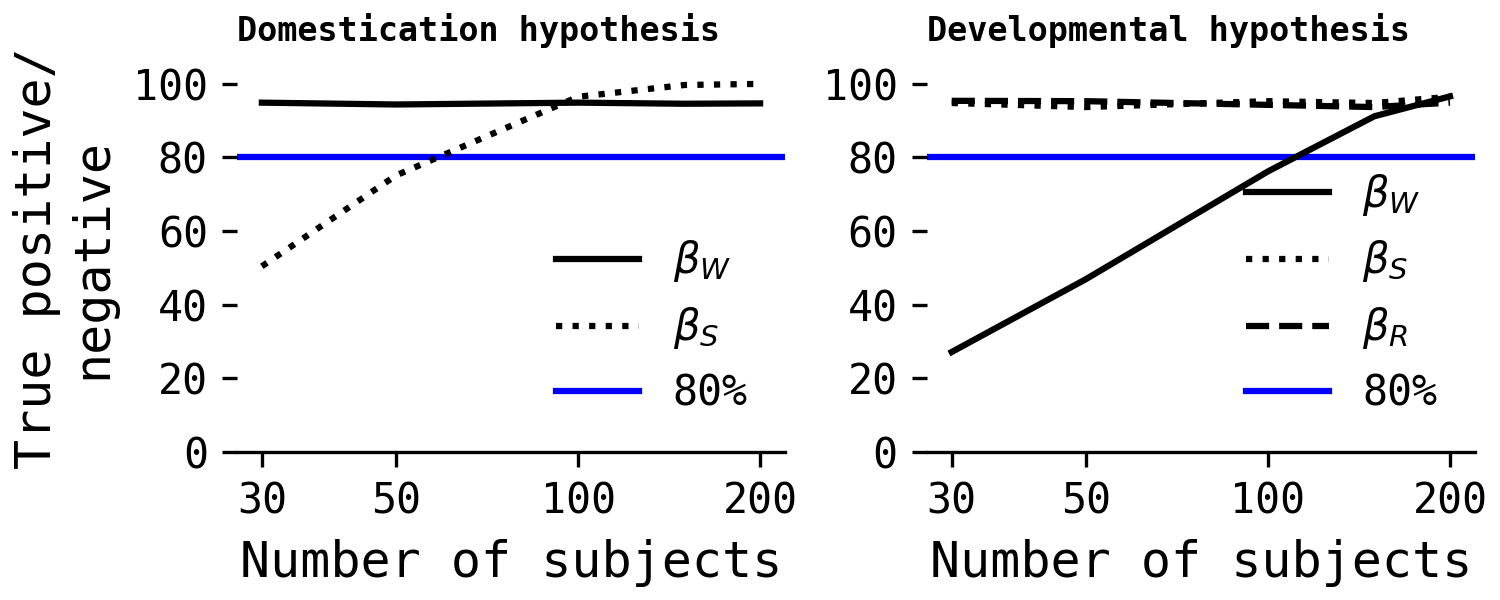
In the left-hand plot, $\beta_S$ is the key parameter of interest, as it represents the only direct casual effect in the domestication hypothesis on point-following. As can be seen, we need at least 50 (25 dogs, 25 wolves) subjects to get close to the traditional 80% threshold of 'ideal power', and as close to 100 subjects as possible for > 80%. For the domestication hypothesis, it appears that Salomons et al. had enough subjects to detect an effect with relatively high probability.

The developmental hypothesis results are less confident. Ideally more than 100 subjects would be needed to achieve 80% power of detecting the true direct effect of $\beta_W$ on point-following performance, and ideally closer to 200 subjects. Why? Estimating the causal effect of willingness to approach in the developmental hypothesis while conditioning on species and rearing experience is harder because species and rearing experience reduce the precision of the effect of willingness. If you want to learn more, check out the ninth model from Cinelli, Forney & Pearl's (2022) good and bad controls paper. While we could just exclude species and rearing experience from that model, entirely, and still estimate the direct causal effect of $\beta_W$, this would make disambiguating the domestication and developmental hypotheses' predictions.

To conclude, then, I don't think there's sufficient evidence to distinguish clearly between the domestication and developmental hypothesis from Salomons et al. study, and Wheat, Bilj & Wynne's re-analysis. Researchers need to decide on the causal assumptions behind these hypotheses and use those assumptions to dictate statistical inference. Someone should re-fit their models including the rearing experience variable from Wheat, Bilj & Wynne to test the domestication hypothesis more clearly, and ideally conduct a replication study with at least 50, if not 75, wolves and dogs. While not a simple task, causal modelling with sufficient power to estimate the causal effects is the surest way to disentangle these two hypotheses.